Prototype |
Représentation des graphes en informatique
Structure associée à la représentation graphique
Un graphe peut être représenté par une liste de sommets, chacun étant caractérisé par son nom, une étiquette éventuelle, et la liste des arcs qui ont ce sommet pour origine (eux-mêmes caractérisés par leur but, et une étiquette éventuelle):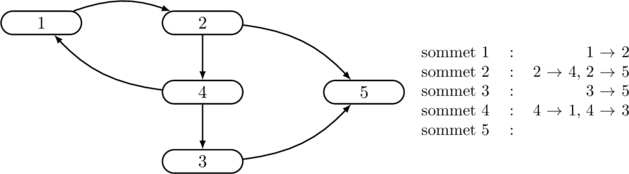
\centerline{{\sc Fig.} \thesection — {\it Représentation par listes d’arcs}}
\addcontentsline{lof}{section}{Représentation par listes d’arcs}
\end{figurette}
Avantages : simplicité de la mise à jour, facilité de parcours; Inconvénients : redondance de la représentation pour les graphes non orientés; temps d’accès aux données (adressage); le parcours ne s’effectue que dans le sens des arcs pour les graphes orientés. (Ce dernier inconvénient peut être supprimé en ajoutant, pour chaque sommet, la liste des arcs qui ont ce sommet pour but, au prix d’un encombrement de la mémoire).
Représentations matricielles
Matrice d’adjacence
Un graphe simple non étiqueté à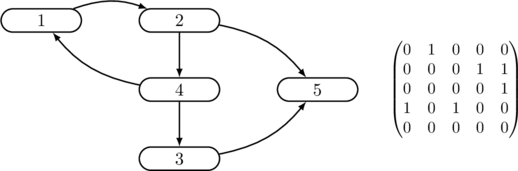
sommets numérotés peut
être représenté par une matrice carrée (, ) d’entiers :
l’élément ![M_{[i, j]}](https://algotaf.dhenin.fr/wp-content/ql-cache/quicklatex.com-094a1cf9d1bcbda7ff538663c5f1dbcd_l3.png "Rendered by QuickLaTeX.com")
vaut 1 s’il existe un arc allant du sommet 
au sommet 
, 0 sinon :
\centerline{{\sc Fig.} \thesubsection — {\it Représentation par matrice d’adjacence}}
\addcontentsline{lof}{section}{Représentation par matrice d’adjacence}
\end{figurette}
Dans le cas où les arcs sont étiquetés, la matrice sera constituée des étiquettes, à condition de pouvoir caractériser l’absence d’arc par une valeur particulière d’étiquette.
Avantages : rapidité des recherches, compacité de la représentation, simplicité des algorithmes de calcul.
Inconvénients : représentation ne convenant qu’aux graphes simples ; redondance des informations pour les graphes non orientés ; stockage inutile de cas inintéressants (les zéros de la matrice), à examiner quand on parcourt le graphe (pour la complexité des algorithmes).
Matrice d’incidence
Un graphe non orienté à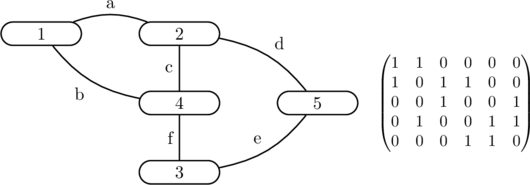 sommets
numérotés et 
arcs numérotés peut être représenté
par une matrice (, ) d’entiers : l’élément
vaut 1 si
le sommet est une extrémité de l’arc , 0 sinon : 
}
\medskip
\centerline{{\sc Fig.} \thesubsection — {\it Représentation par matrice d’incidence}}
\addcontentsline{lof}{section}{Représentation par matrice d’incidence}
\end{figurette}
Dans le cas où les arcs sont étiquetés, la matrice
sera constituée des étiquettes, à condition de pouvoir
caractériser l’absence d’arc par une valeur particulière
d’étiquette. Avantages : rapidité des recherches, compacité de la représentation, informations non redondantes pour les graphes non orientés ; Inconvénients : stockage et examen inutile de zéros; les calculs de matrices classiques ne s’appliquent pas.
