Les structures

Prototype


Suppression/Insertion d’un maillon de liste
Page Suivante

Généralités

Par extention du sens habituel donné au mot, une liste\footnote{Les listes peuvent être vues comme des formes simples d’arbres (cf. page \pageref{Arbre}) ; on peut en effet considérer qu’une liste est un arbre binaire dans lequel tout fils gauche est une feuille. linéaire\footnote{Knuth distingue les « listes linéaires » des « listes » au sens large qui désignent plus complexes ({i.e.} arborescentes). Cependant l’usage ne maintient pas cette distinction.} est un type de données abstrait comprenant une suite d’informations (données) ainsi que les opérations (méthodes) nécessaires au maniement de ces données. La liste est une structure de base de la programmation\footnote{Le langage {sc lisp}, conçu par John MacCarthy en 1960, utilise pricipalement cette structure qui se révèle utile pour le calcul symbolique.}. Chaque élément permet l’accès à deux valeurs : l’objet associé à cet élément et l’élément suivant\footnote{Le numéro de ligne, lorsqu’il s’agit d’un tableau, comme dans la figure ??, l’adresse en mémoire, lorsqu’il s’agit de pointeurs.}. La recherche d’un élément dans la liste s’apparente à un « jeu de piste » dont le but est de retrouver un objet caché : on commence par avoir des informations sur un lieu où pourrait se trouver l’objet, en ce lieu on découvre des information sur un autre lieu où il a une chance de se trouver et ainsi de suite. Une liste doit pouvoir être modifiée : on doit être capable de supprimer ou d’ajouter des données. Pour accéder à une donnée appartenant à une liste, il convient de disposer de la liste mais aussi de la place (position) de cette donnée dans la liste. Une liste peut être vide ; on peut vider une liste ; on peut accéder au ième élément, en connaître le contenu ; on peut connaître la longueur de la liste (le nombre d’éléments qu’elle contient) ; on peut supprimer un élément de la liste, y insérer un nouvel élément et enfin accéder au successeur d’un élément dont on connaît la place. Enfin, on peut vouloir fabriquer une liste à partir de deux autres. La pile (LIFO)} est une liste dans laquelle on insère et on supprime seulement à une extrémité ; La file (FIFO)} est une liste dans laquelle on insère à une extrémité et où on supprime à l’autre. Il existe de nombreuses façons de mettre en œuvre les listes. La mise en œuvre dans un tableau facilite la compréhension, mais présente l’inconvénient de ne contenir qu’un nombre maximum de cellules prédéfini.

Mise en œuvre des listes dans un tableau

La figure ?? montre un tableau {\tt ESPACE} contenant deux listes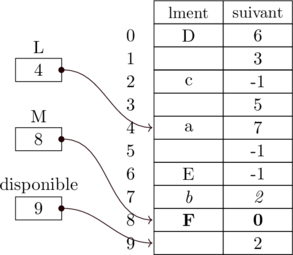 {\cal L} = a, b, c et {\cal M} = D, E. Pour chainer les éléments des listes on utilise un vecteur « suivant » de faux-pointeurs, c’est à dire le numéro de ligne du successeur. Remarquez que toutes les cellules du tableau n’appartenant à aucune des deux listes sont chaînées en une pile\footnote{Cf. page \pageref{Pile}.} appelée {\bf disponible}. Cette liste supplémentaire sert à trouver un espace libre pour insérer un nouvel é­lé­ment, ou à récupérer les espaces libérés par la suppression d’éléments précé­dem­ment dans une liste en vue d’une utilisation ultérieure.

Rendered by QuickLaTeX.com

La variable L contient l’indice de ligne où commence la liste {\cal L} et la variable M celui de la liste {\cal M} ; la case ESPACE[L][element] contient le premier élément (a) et ESPACE[L][suivant] l’indice du successeur (8) c’est-à-dire b. De la même façon, ESPACE[8][suivant] contient 3. c n’ayant pas de successeur, il est le dernier élément, ESPACE[3][su­i­vant] est -1.

Programmation d’une liste générique

La totalité des sources du TDA liste est donné en annexe.
Le fichier d’entête du TDA liste (Liste.h), contient la définition de 3 structures :
  • La structure cellule, qui contient un pointeur sur la donnée associée et un pointeur sur la cellule suivante,
  • la structure de tête qui donne accès à la première cellule de la liste, à la dernière et à la cellule courante (vue),
  • structure donnant accès aux méthodes (fonctions\footnote{Voir les pointeurs de fonction p. ??}). 
#define LISTE_H
#include 
#include 

#define nom(a,b) a##b

typedef struct cell
{
    void        * objet ;
    struct cell * suiv  ;
} * cellule ;

typedef struct tete
{
    cellule prem, vue, der, s ;
} * liste ;

extern void * lier_liste () ;
struct fonctions
{
    liste  (*creer)      ()                         ;
    void   (*copier)     (void *)                   ;
    void   (*detruire)   (liste, void (*) (void*))  ;
    int    (*nulle)      (liste)                    ;
    void   (*premier)    (liste)                    ;
    void   (*dernier)    (liste)                    ;
    void   (*suivant)    (liste)                    ;
    int    (*fin)        (liste)                    ;
    void * (*lire)       (liste)                    ;
    void   (*insereravant) (liste, void *)          ;
    void   (*insererapres) (liste, void *)          ;
    void   (*remplacer)  (liste, void *, void (*) (void*)) ;
    void   (*oter)       (liste, void (*) ())       ;
    void   (*fixer)      (liste)                    ;
    int    (*retablir)   (liste)                    ;
    void   (*afficher)   (liste, void (*) ())       ;
} Liste ;
Les structures
Suppression/Insertion d’un maillon de liste
Page Suivante