Algotaf cartographie mentale |
Ensembles binaires algébriques
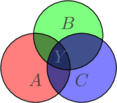
Conjonction ensemblistes
La conjonction est représentée par l'intersection des ensembles et s'écrit en algèbre de Boole ![]() .
.
Fonctions binaires
On appelle variable ou fonction binaires, toute variable ou toute fonction ne pouvant prendre que l'une des deux valeurs algébriques distinctes ![]() , à l’exclusion de toute autre.
, à l’exclusion de toute autre.
L'ensemble « ![]() » des variables et des fonctions ainsi définies est appelé ensemble binaire algébrique.
» des variables et des fonctions ainsi définies est appelé ensemble binaire algébrique.
Le choix de l'ensemble ![]() se justifie par l'adoption d'une valeur d'absorption «
se justifie par l'adoption d'une valeur d'absorption « ![]() » et d'une valeur neutre
» et d'une valeur neutre ![]() »
»
![]()
Produit
Les expressions conjonctives sont utilisées dans différents contextes : pour les commentaires, dans les évaluations d'expressions, dans la fabrication des ordinateurs notamment dans les unités centrales…
Conjonction en programmation
... 01 coup = 1 02 while /* secret pas devine et coup < 3 */ 03
Conjonction en logique
Une assertion conjonctive est de la forme : ![]() et
et ![]() . Nous écrivons
. Nous écrivons ![]() ou
ou ![]() , ce que certains auteurs notent :
, ce que certains auteurs notent : ![]() ,
, ![]() ou
ou ![]() and
and ![]() .
.
Supposons qu'une telle proposition, par exemple dans le programme ci-dessus « Le secret n'est pas deviné et l'on a fait moins de 3 essais » soit vraie. L'usage habituel de la conjonction « et » est tel que nous entendons que, d'une part, « Le secret n'est pas deviné » et, d'autre part, « on a fait moins de 3 essais » sont toutes deux des assertions vraies. Ceci conduit à poser les règles d'élimination suivantes :
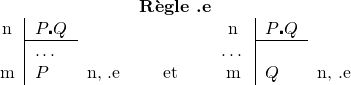
À la ligne 04, nous faisons l'hypothèse ![]() , « secret pas devine et coup < 3 », donc à la ligne 10, nous pouvons éliminer
, « secret pas devine et coup < 3 », donc à la ligne 10, nous pouvons éliminer ![]() et écrire l'assertion « code pas devine' ».
et écrire l'assertion « code pas devine' ».
Cela tombe sous le sens. Inversement d'ailleurs, dans le cas où l'on sait que deux assertions ![]() et
et ![]() sont vraies séparément, nous sommes disposés à affirmer que la proposition conjonctive
sont vraies séparément, nous sommes disposés à affirmer que la proposition conjonctive ![]() est aussi vraie. D'où la règle d'introduction :
est aussi vraie. D'où la règle d'introduction :
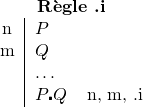
Conjonction en algèbre binaire
Soit ![]() fonctions binaires
fonctions binaires ![]() telles que
telles que ![]() , le produit algébrique de ces
, le produit algébrique de ces ![]() fonctions appartient à l'ensemble
fonctions appartient à l'ensemble ![]() .
.
![]()
Le produit
![]()
Il est nul dans tous les autres cas.
Conjonction électriques
Nous appellerons également le produit « ![]() » fonction et quand il fera l'objet d'application technologiques.
» fonction et quand il fera l'objet d'application technologiques.
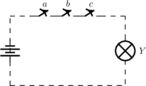
Fonction « et » — produit ![]()
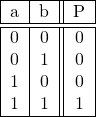
Conjonction et table de vérité
Le calcul de la valeur de ![]() peut se synthétiser dans la table de vérité ci-dessous :
peut se synthétiser dans la table de vérité ci-dessous :