Prototype |
Définition
Un arbre est une structure qui est :- soit vide\footnote{que nous noterons
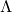 .
Concrètement,
.
Concrètement, 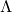 pourra être 0, -1 ou tout
autre valeur significative dans un contexte particulier.},
pourra être 0, -1 ou tout
autre valeur significative dans un contexte particulier.},
- soit composée d’un {\em n\oe ud} chaîné à zéro un ou plusieurs sous-arbres ordonnés de gauche à droite.

Étiquettes et expressions
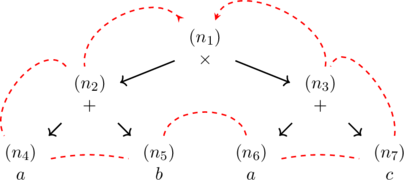
L’arbre étiqueté de la figure ?? représente l’expression arithmétique- Chaque feuille est étiquetée par un opérande et est constituée de cet
opérande uniquement. Ainsi la feuille
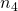 représente l’expression
représente l’expression  .
.
- Chaque nœud interne
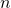 est étiqueté par un opérateur. Si
est étiqueté par un opérateur. Si 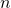 est étiqueté par un opérateur binaire
est étiqueté par un opérateur binaire 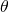 , comme
, comme 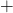 ou
ou  , si son
fils gauche représente l’expression
, si son
fils gauche représente l’expression 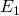 et son fils droit
l’expression
et son fils droit
l’expression 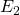 , alors
, alors 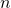 représente l’expression (
représente l’expression (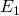 )
)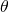 (
(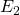 ). Les parenthèses peuvent être retirées si aucune
ambiguïté n’est à craindre.
). Les parenthèses peuvent être retirées si aucune
ambiguïté n’est à craindre.
Parcours d’arbres
Il existe plusieurs moyens de parcourir les nœuds d’un arbre. Les trois parcours les plus importants sont les parcours préfixé, {postfixé et infixé ; ces parcours peuvent être définis récursivement.Il existe un moyen pratique pour simuler les trois parcours d’arbre : imaginons que l’on parcourt l’arbre depuis sa racine, dans le sens contraire à celui des aiguilles d’une montre, en en restant toujours le plus près possible.