Longs

Prototype


012_Quinze_vainc
Page Suivante
Le problème du choix d’un itinéraire (??) pourrait être résolu en examinant tous les ordonnancements possibles des sommets au départ de Bordeaux ; si l’on part d’un graphe à n sommets, cela donne n! possibilités, ce qui conduit à un algorithme irréalisable, en pratique.
L’algorithme de Little
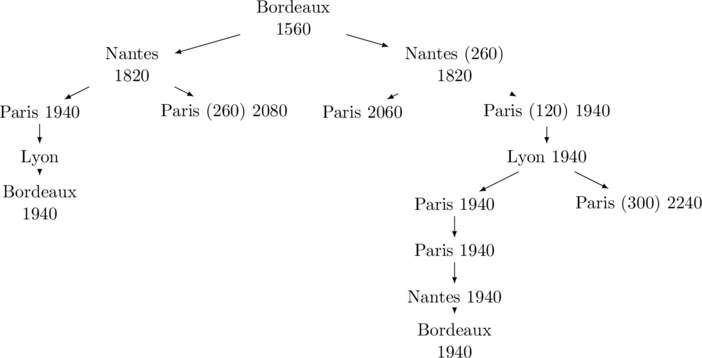
L’algorithme de Little est du type « séparation et évaluation » : on effectue un parcours en profondeur de l’arborescence binaire des choix possibles, en attribuant à chaque nœud n une évaluation par défaut e_{(n)}, et une valeur de regret à chaque choix auquel on renonce (évaluation par défaut du prix à payer pour renoncer à ce choix).
On remarque tout d’abord que l’on ne change pas le problème en soustrayant un nombre quelconque à une ligne ou une colonne de la matrice des distances entre les villes (cela revient à soustraire cette distance à tous les circuits hamiltoniens). On appellera réduction de la matrice l’opération consistant à soustraire de chaque ligne le plus petit élément, puis à soustraire le plus petit élément de chaque colonne de la matrice ainsi obtenue.
L’évaluation par défaut associée à la racine de l’arborescence est la somme des nombres soustraits lors de cette réduction.
Chaque nœud de l’arborescence correspond à un choix (fait ou abandonné). L’évaluation par défaut associée à un nœud de type « choix fait » est la somme de l’évaluation par défaut associée au nœud père, et d’une évaluation par défaut du chemin restant à parcourir (obtenue par réduction de la matrice des liaisons encore possibles) ; il faut prendre soin d’éliminer les liaisons créant des circuits parasites, par exemple Nantes-Bordeaux si l’on a déjà choisi d’emprunter Bordeaux-Lyon et Lyon-Nantes).
Le regret associé à un choix abandonné est calculé de la façon suivante : si on renonce à une liaison s \rightarrow t, il faudra sortir de s et entrer dans t par d’autres liaisons ; la valeur de regret associée à s \rightarrow t est la somme du plus petit coût des liaisons s \rightarrow s' et du plus petit coût des liaisons t' \rightarrow t encore disponibles.
L’évaluation par défaut associée à un n\oe ud de type « choix abandonné » est la somme du regret et de l’évaluation par défaut du nœud père.
On parcourt l’arborescence en profondeur, en ignorant les nœuds dont l’évaluation par défaut dépasse la valeur d’un circuit hamiltonien déjà trouvé. 
algorithme de Little :
 maxi = +inf 
 s[racine] = ville de depart
 calculer e[racine]
 visiter la racine

visiter un noeud n :
 SI e[n] <= maxi
 ALORS
  SI s[n] != ville de depart
  ALORS
   POUR toutes les liaisons s[n] -> v possibles
    calculer le regret de s[n] -> v
   FIN POUR 
   soit s[n] -> v une liaison de
   regret maximal r
   créer les fils v et V de n
   s[v] = v
   calculer e[v]
   visiter v
   s[V] = s[n]
   e[V] = e[n] + r
   visiter V
  SINON
   maxi = max[maxi, e[n])
  FIN SI
 FIN SI

Rendered by QuickLaTeX.com

Longs
012_Quinze_vainc
Page Suivante