Complexité |
Temps et espace d’exécution
Le temps d’exécution et la place mémoire requise caractérisent la complexité d’un programme. Sous UNIX, on mesure le temps d’exécution d’un programme au moyen de la commande time.:; time wc session/log 31 136 1044 session.log real 0m0.08s user 0m0.01s sys 0m0.02sIl tombe sous le sens qu’un programme mettra d’autant plus de temps à s’achever qu’il aura de données à traiter. Pour un même résultat, deux algorithmes équivalents ne verront sans doute pas leur temps d’exécution croître dans les mêmes proportions en fonction desdonnées à traiter. Exemple : Calculs du plus grand diviseur de
i = n - 1 ;
while (0 != (n % i))
/* pgd ≤ i const. de boucle */
i = i - 1 ;
pgd = i ;
Deuxième méthode :
i = 2 ; while (i <et 0 != (n % i)) /* pgd > i const. de boucle */ i = i + 1 ; /* pgd = SI (
modulo
) ALORS
SINON 1 */ pgd = (0 == (n % i)) ? n/i : 1 ;
- Complexité en tempsLa complexité d’un algorithme se mesure essentiellement en calculant le nombre d’opérations élémentaires pour traiter une donnée de taille. Les opérations élémentaires considérées sont
- le nombre de comparaisons (algorithmes de recherches)
- le nombre d’affectations (algorithmes de tris)
- Le nombre d’opérations (
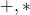 ) réalisées par l’algorithme (calculs sur les matrices ou les polynômes).
) réalisées par l’algorithme (calculs sur les matrices ou les polynômes).
 pour une donnée
pour une donnée 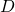 est le nombre d’opérations élémentaires nécessaires au traitement de la donnée
est le nombre d’opérations élémentaires nécessaires au traitement de la donnée 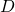 et est noté
et est noté 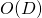
- Complexité dans le pire des cas,
exemple : recherche d’un nombre dans un tableau, alors qu’il n’y est pas :
![Rendered by QuickLaTeX.com \[ \mbox{Max}_{(n)} = \mbox{max}\{O(d_{1}), d_{i}\in D_{i} \} \]](https://algotaf.dhenin.fr/wp-content/ql-cache/quicklatex.com-fec3936e078ce7084919bf40b959ef26_l3.png)
- Complexité dans le meilleur des cas,
ex : rechercher d’un nombre dans un tableau, alors qu’il est en première position :
![Rendered by QuickLaTeX.com \[ \mbox{Min}_{(n)} = \mbox{min}\{O(d_{1}), d_{i}\in D_{i}\} \]](https://algotaf.dhenin.fr/wp-content/ql-cache/quicklatex.com-e3b357a424c411955028ea99016b601d_l3.png)
- Complexité en moyenne
![]()
![]()
- Espace mémoire
Calcul de complexité d’un algorithme :
apparition d’un nombre dans un tableau. Soitint Trouve (int T[], int n, int a)
{
int i = 0 ;
while (i \le n)
if (T[i] == a )
return i ;
/* i == n ; le tableau est parcouru */
return 0 ;
}
Cas le pire : De fait les cas où l’on peut explicitement calculer la complexité en moyenne sont rares. Cette étude est un domaine à part entière de l’algorithmique
Analyse asymptotique
- Analyse du temps d’un calcul d’un programme
- Valeur approchée Le temps de calcul d’un programme dépend trop de la vitesse de l’ordinateur et du compilateur utilisés. On peut donc calculer les performances d’un algorithme à facteur multiplicatif constant. Des programmes de complexités
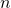 ,
, 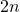 ou
ou 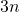 sont quasiment équivalents.
sont quasiment équivalents. - Règle des 90/10 : 90% du temps de calcul d’un programme est réalisé dans 10% du code. Inutile donc d’essayer de perdre trop de temps à optimiser les 90% qui ne prennent que 10% du temps. Autant se consacrer à ce qui est le plus pénalisant.
- Exemple : comparaisons d’un algorithme
 de complexité
de complexité 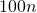 et d’un algorithme
et d’un algorithme 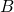 de complexité
de complexité 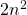 (cf Aho-Ullman)
(cf Aho-Ullman)
- Valeur approchée Le temps de calcul d’un programme dépend trop de la vitesse de l’ordinateur et du compilateur utilisés. On peut donc calculer les performances d’un algorithme à facteur multiplicatif constant. Des programmes de complexités
- Notations
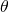 et
et 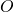 :
:
- Définitions. On dit que
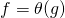 lorsqu’il existe deux constantes
lorsqu’il existe deux constantes 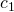 et
et 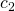 positives (
positives ( 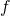 et
et 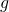 sont également supposées à valeurs positives) telle que, pour
sont également supposées à valeurs positives) telle que, pour 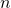 assez grand
assez grand
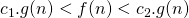 Remarquons que cette relation est réflexive.
Remarquons que cette relation est réflexive. - On dit que
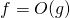 lorsqu’il existe une constante
lorsqu’il existe une constante  positive telles que, pour n assez grand
positive telles que, pour n assez grand
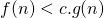 c’est dire que
c’est dire que 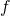 est bornée par
est bornée par 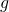 à un facteur multiplicatif près.Cette relation n’est pas réflexive.
à un facteur multiplicatif près.Cette relation n’est pas réflexive. - Propriétés.Un polynôme est de l’ordre de son degré. On distingue les fonctions linéaires (en
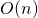 ), les fonctions quadratiques (en
), les fonctions quadratiques (en 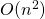 ) et les fonctions cubiques (en
) et les fonctions cubiques (en 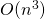 ).Les fonctions d’ordre exponentiel sont les fonctions en
).Les fonctions d’ordre exponentiel sont les fonctions en 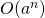 ou
ou 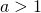 .Les fonctions d’ordre logarithmique sont les fonctions en
.Les fonctions d’ordre logarithmique sont les fonctions en 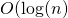 ) (Remarquons que peu importe la base du logarithme).
) (Remarquons que peu importe la base du logarithme). - Une classe intéressante d’algorithme est en
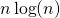 . Comparaison de
. Comparaison de 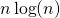 et de
et de 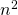 .
. - Comparaison des asymptotiques classiques.
- Rappelons que
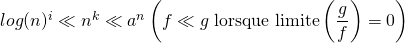 .
. - Fractions rationnelles
- Factorielle : formule de Stirling
- Nombres de Fibonacci
- Rappelons que
- Calcul de complexité dans les structures de contrôle.
- Les instructions élémentaires (affectations, comparaisons) sont en temps constant, soit en
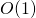 .
. - Tests :
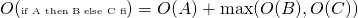
- Boucles
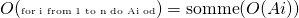 .
Lorsque
.
Lorsque 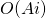 est constant à
est constant à 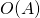 , on a
, on a 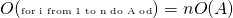
- Cas particuliers : boucles imbriquées
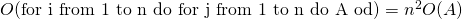
- Le fait que la borne sup de la boucle intérieure soit
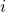 plutôt que
plutôt que 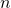 ne change rien :
ne change rien : 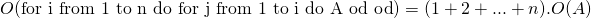 .
.
- Les instructions élémentaires (affectations, comparaisons) sont en temps constant, soit en
- Définitions. On dit que

