Prototype |
Parcours de graphes
Les algorithmes de parcours des arborescences s’adaptent aux graphes, en considérant que l’on parcourt chacune des arborescences associées aux sommets du graphe ; l’arborescence associée à un sommet est celle des descendants de ce sommet que l’on n’a pas encore visités.Parcours en largeur
parcourir un graphe en largeur :
visiter tous les sommets
visiter un sommet s :
SI s n'a pas encore ete enfile
ALORS enfiler s ;
TANT QUE la file nest pas vide
soit n le premier sommet de la file ;
{traitement de n}
defiler ;
enfiler tous les successeurs
non encore enfiles de n
FIN TANT QUE
FIN SI
|
tant que, on défile un sommet
différent, donc chaque procédure visiter se termine. À la
sortie de visiter, la file est vide ; donc chaque sommet aura été
défilé, et par conséquent traité, exactement 1 fois.
Complexité : Chaque sommet est traité 1 fois, et chaque arc est
examiné 1 fois (lors du traitement de son origine). La complexité
est donc de l’ordre de Parcours en profondeur (récursif)
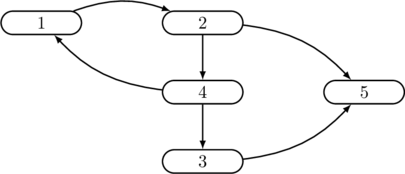
\medskip\centerline{{\sc Fig.} \thesubsection — {\it Ordre de visite : 1, 2, 4, 3, 5 ;}}
\centerline{\it de post-visite : 1, 5, 3, 4, 2}
\addcontentsline{lof}{section}{Ordre de visite et de post-visite}
\end{figurette}
parcourir un graphe en profondeur :
visiter tous les sommets
visiter un sommet s :
SI s n'a pas encore ete visite
ALORS
{pre-traitement de s}
visiter tous les successeurs de s
{post-traitement de s}
FIN SI
|

