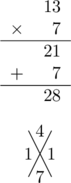Algorithme |
Algorithme « papier » ou « réel » programme
Bien entendu, on peut réfléchir avec un papier et un crayon.
Cependant, le débutant n’imagine pas encore les détails qui rescellent le diable. Par conséquent, il est très utile de pourvoir se confronter à la surdité et à la stupidité de l’ordinateur et garder son humour jusqu’à trouver un terrain d’entente : un langage commun (algobox, python, java ? ) un vocabulaire sans ambiguïté (%, mod, ? <-; := ou = ?) et une syntaxe ( Real N, N number, ...)
-
-
- Un algorithme est une succession de manœuvres à accomplir toujours dans le même ordre et de la même façon, manœuvres qui sont en nombre fini et s’appliquent à un nombre fini de données. Par exemple, on connaît depuis l’enfance des algorithmes de calcul, ceux qui permettent de trouver ce que vaut la somme, le produit, la différence ou le quotient de deux nombres quand ils s’écrivent avec plus d’un chiffre. Il ne s’agit pas d’autre chose quand on entend dire « je ne sais plus faire une division », par exemple celle de 793 par 32 ; en fait, c’est l’algorithme de calcul du quotient qu’on n’a plus en mémoire, c’est-à-dire le « j’ai deux chiffres au diviseur, j’en prends deux au dividende, je dis en 79 combien de fois 32 ou en 7 combien de fois 3, il y va deux fois, etc »
- Les livres donnent volontiers comme exemples d’algorithmes ceux qui consistent à trouver le nouveau prix d’un objet s’il y a, au moment de l’achat, une baisse ou une hausse de, mettons, 10 % ; si le prix initial est
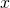 , la hausse ou la baisse est les
, la hausse ou la baisse est les 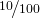 de
de 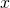 , soit
, soit 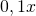 ; le nouveau prix est donc :
; le nouveau prix est donc :
- en cas de baisse :
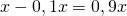 ,
, - en cas de hausse :
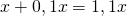 .
.
- en cas de baisse :
- Un algorithme est généralement répétitif ; c’est le cas si on place une somme d’argent à la banque à un taux de 4 % ; au bout d’une année, elle devient les 104/100 de ce qu’elle était, au bout de deux années les 104/100 des 104/100 de ce qu’elle était, etc.
En désignant cette somme par S, on a donc, au bout
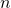 années, une somme :
années, une somme :
![Rendered by QuickLaTeX.com \[ S_n = \underbrace{(\nicefrac{104}{100}) (\nicefrac{104}{100})\ldots(\nicefrac{104}{100})}_{n\mathrm{ fois}}S=1,04^n S \]](https://algotaf.dhenin.fr/wp-content/ql-cache/quicklatex.com-2cdbe75d9480eec78a9644e4b4738ccb_l3.png)
- On désigne par algorithme un procédé automatique que l’on peut confier à un ordinateur et qu’il répétera autant de fois qu’il le faudra pour arriver au résultat. Imaginons qu’on l’ait programmé pour la suite d’opérations suivantes : à partir d’un entier naturel
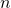 quelconque, si
quelconque, si 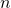 est pair le diviser par 2 ; s’il est impair, prendre son triple et ajouter 1, c’est-à-dire fabriquer
est pair le diviser par 2 ; s’il est impair, prendre son triple et ajouter 1, c’est-à-dire fabriquer 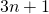 ; dans chaque cas, recommencer avec le nouveau nombre obtenu. Essayons avec quelques nombres :
; dans chaque cas, recommencer avec le nouveau nombre obtenu. Essayons avec quelques nombres :
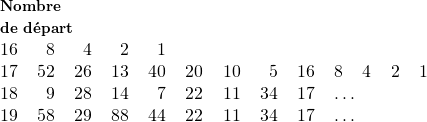 Il est clair qu’en arrivant à 1, le processus va ‘se boucler’ sur lui-même, puisqu’on aura la suite 1, 4, 2, 1, 4, 2, 1, etc. On voit que c’est ce qui se produit pour 16 et 17 ; or, pour 18 et 19, on retombe sur 17, donc on arrivera aussi à 1.La conjecture qui s’établit à partir de plusieurs tentatives qui, toutes, amènent à 1 est que, quel que soit le nombre de départ et le nombre d’étapes, cet algorithme produira toujours 1 ; mais elle n’est, malgré son apparente simplicité, toujours pas démontrée aujourd’hui. Ce ‘beau’ problème s’appelle « le problème de Collatz », du nom du professeur de Hambourg qui l’a lancé [G
Il est clair qu’en arrivant à 1, le processus va ‘se boucler’ sur lui-même, puisqu’on aura la suite 1, 4, 2, 1, 4, 2, 1, etc. On voit que c’est ce qui se produit pour 16 et 17 ; or, pour 18 et 19, on retombe sur 17, donc on arrivera aussi à 1.La conjecture qui s’établit à partir de plusieurs tentatives qui, toutes, amènent à 1 est que, quel que soit le nombre de départ et le nombre d’étapes, cet algorithme produira toujours 1 ; mais elle n’est, malgré son apparente simplicité, toujours pas démontrée aujourd’hui. Ce ‘beau’ problème s’appelle « le problème de Collatz », du nom du professeur de Hambourg qui l’a lancé [G ].
].
-
- Algorithme s’est d’abord dit algorisme, du bas latin algorismus, déformation d’après le mot grec arithmos, « nombre », et du nom propre Al-Khwarizmi.
| – Vingt-huit divisé par sept : en 8 combien de fois 7 ? Il y va une fois. Une fois sept fait 7 ; ôté de 8 il reste 1. J’abaisse le 2. En 21 combien de fois 7 ? Il y va 3 fois. 3 fois 7 font 21 ; ôté de 21, il reste 0. Tu mettras donc 13 moutons dans chaque bergerie. – Bien, père, fit le Toine, convaincu par la science. | |
| Il partit incontinent, pour procéder à la répartition.Une heure plus tard, Mathieu le vit revenir tout piteux : – J’y arrive pas, père. Il doit y avoir une erreur. – Écoute-moi bien, lui dit son père. Y a pas d’erreur possible. D’ailleurs pour te le prouver, on va procéder autrement. Je t’ai dit 13 moutons dans chaque bergerie. Si on multiplie 13 par 7, on doit retrouver les 28 têtes. Allons-y : | |
| Treize multiplié par sept : 7 fois 3 font 21 ; et 7 fois 1 fait 7. Tu vois que 21 et 7, ça fait bien 28. D’ailleurs, pour être plus sûr, on va faire la preuve par neuf : 3 et 1 font 4. Je pose 4 en haut et j’écris 7 en dessous. 7 fois 4 font 28. 8 et 2 font 10. J’écris 1 à gauche. Maintenant le résultat : 8 et 2 font 10. J’écris 1 à droite. Tu vois bien que c’est juste. Allez, va-t-en me mettre treize bêtes dans chaque bergerie.(Ici, normalement, Mathieu aurait dû s’inquiéter, puisque 7 fois 13, comme 7 fois 4 font également 28. Mais s’il fallait encore s’attacher à tant de menus détails, on n’avancerait jamais. On continua donc). |
|
| C’est un Toine effondré qui revint une heure plus tard. – J’y arrive toujours pas. Y a sûrement quelque chose qui ne va pas dans les comptes. – Y a surtout qu’t’es pas bien malin, fils, dit le père Mathieu. La division, la multiplication, c’est trop fort pour toi. L’addition, ça doit aller mieux. | |
| J’écris 13, sept fois de suite, et j’additionne : 3 et 3, 6 ; et 3, 9 ; et 3, 12 ; et 3, 15 ; et 3, 18 ; et 3, 21 ; et 1, 22 ; et 1, 23 ; 24 ; 25 ; 26 ; 27 ; 28. Es-tu convaincu, cette fois ? Allez, va. Et le Toine repartit encore une fois, loger les maudites bêtes. | |
| Et en fin de soirée, il revint triomphant. – Ça y est, père, tous les moutons sont rentrés ! – Comment que t’as fait ? – Je les ai fait rentrer un par un en faisant le tour des bergeries. Et pour être tout à fait sûr, quand ils ont été placés, moi aussi, j’ai fait mes comptes : j’ai compté les pattes ; j’ai trouvé 16 pattes dans chaque bergerie. | |
| – Attends voir, dit le Père Mathieu. Faut pas s’emballer. Étant donné qu’un mouton a 4 pattes, si je divise 16 par 4, je saurai combien tu as mis de bêtes dans chacune. Et la nouvelle division fut posée : seize divisé par quatre : en 6 combien de fois 4 ? Il y va une fois. Une fois 4 fait 4 ; ôté de 6, il reste 2. J’abaisse mon 1. En 12 combien de fois 4 ? Il y va 3 fois. 3 fois 4 font 12 ; ôté de 12, il reste 0. | |