Algorithmique sans problème ?

Jean-Jacques Dhénin

17 Novembre 2009

Version pdf

Résumé

En réplique aux idées reçues à propos de l’algorithmique, nous allons porter notre attention sur deux procédés pratiques pour l’enseignement de l’algorithmique en seconde :

• La table d’analyse  qui systématise la construction de l’algorithme et économise le temps de recherche.

• Les assertions qui indiquent les relations entre les variables et valident l’algorithme ; placées en commentaires, elles traduisent et donnent le sens du fonctionnement du programme.

Il s’agit bien de deux approches complémentaires qui prétendent fournir l’assise de l’algorithmique.

1 Posons le problème (le temps de voir)

Notre génération se trouve mise en présence aujourd’hui avec l’enseignement de l’algorithmique. Pour l’heure, les opinions divergent et toutes les directions ne se valent pas [Dhenin1]. Comme pour enseigner les mathématiques, cela suppose une réflexion sur les objectifs de la discipline [Bkouche] : qu'allons-nous enseigner et dans quel but ?

Essayons de comprendre les questions. Nous en connaissons vraisemblablement un bout puisque nous utilisons déjà le mot, algorithme [1] .

Un objectif mal défini se traduit ...  ... toujours par une erreur précise.

D’autre part, la lecture des divers documents mis à notre disposition nous renseigne sur la commande sociale [Eduscol]. Ce qui est frappant dans cette prescription, c’est le fait que l’enseignement de l’informatique n’est pas indiqué comme transmission de connaissances mais, au mieux, comme une pratique. Pourtant, l’avenir ne devrait pas se réduire à un aménagement du présent et prévoir certaines difficultés pourrait nous épargner bien des tracas.

Qu’est-ce qui est vain ? Apprendre sans réfléchir ou réfléchir sans apprendre ? Considérons plutôt que notre métier, entre autres, consiste à transmettre des connaissances aux élèves. Cela ne signifie ni un désintérêt pour les élèves, ni un dédain pour la pédagogie. C’est bien plutôt que le sens, en pédagogie, commence en amont, il est intrinsèque à la discipline elle-même.

Donnons au problème une forme telle qu’il soit possible de le résoudre [Vuillemin].

Certains obstacles en mathématiques, pour nos élèves, sont en fait des difficultés de français : ils comprennent mal nos énoncés et notre enseignement.

C’est ce que dit depuis fort longtemps Stella Baruk [Leguay].

Nous devrions être toujours prudents de nos mots et de tout ce qu’ils portent comme sens usuel [2] .

L’algorithmique apporte un nouveau vocabulaire qui nécessite d’autant plus d’explications qu’il n’est pas d’usage quotidien pour la majorité des élèves. Les mots entrer, réitérer, valeur de n, tester, itération, étape, modulo, initialiser, remplacer, expliciter, commentaires, instructions, présupposition... peuvent sembler avoir un sens évident, pour qui pratique la programmation, pas pour le débutant [3] . Nous prendrons soin de n’en faire usage qu’après nous être assurés d’être compris. Éclairer n’est pas éblouir.

Considérons, par exemple, le mot « affectation » utilisé par la programmation impérative, la plus répandue (Fortran, Pascal, C,...) et la plus proche de la machine réelle. Son principe est de modifier à chaque instant l’état de la mémoire via les affectations.

Ce mode de programmation présente plusieurs défauts pour un lycéen quelle que soit l’écriture retenue [4] . . .

• Dès lors, on ne peut plus parler de la valeur de la variable x. Il faut parler de la suite des valeurs que prend cette variable, et l’on ne peut en rendre compte correctement qu’en reprenant le mécanisme exact d’exécution du programme.

« Un instant, S.V.P. ! Hier vous disiez que x valait 2 ! »

Ce n’est pas là le seul inconvénient de l’affectation ; on s’éloigne des mathématiques en utilisant l’affectation comme base de programmation : un élève de seconde découvre les fonctions qui à un nombre donné associent une unique image, comment comprendra-t-il qu’une même variable peut prendre des valeurs tout à fait différentes selon le moment où on l’évalue ? Une expression mathématique, telle que y = 5x + 3 sous-entend que la valeur d’y dépend de celle d’x. Si nous connaissons x nous pouvons connaître y. De même en algorithmique si y ← 5x + 3 ne présente pas de difficulté pour moi, pour l’élève la difficulté réside dans l’inversion du sens de la flèche. La flèche n’a plus le même sens. Que dire de et de x ← 5x + 3 ? Bien sur si l’on ne se fonde que sur les élèves « mordus d’informatique » on aura l’illusion d’être compris ; mais chacun sait ...

• une variable peut être modifiée en plusieurs endroits du programme, et cela est vraiment une grande source de difficultés dans la programmation impérative.

Mieux vaut allumer une bougie que maudire les ténèbres [Lao Tseu].

Or il y a trois modes de programmation : la programmation constructive (ou impérative, celle qui utilise l’instruction d’affectation), la construction implicite (ou récursive, ou fonctionnelle, ou explicative...) et la programmation logique. Ce sont trois modes de pensée différents. Pour chaque mode, il y a différentes méthodes pour élaborer un programme.

La documentation, déjà conséquente, sur ce sujet, par exemple [Sesamath], montre que la programmation fonctionnelle s’affranchit de façon radicale des effets de bord [5] en interdisant toute opération d’assignation ; malheureusement, la programmation fonctionnelle n’est pas au programme de seconde générale pour l’instant.

L’importation de ces méthodes (produites par les pratiques professionnelles) dans des situations d’enseignement est délicate. Une part de la difficulté réside dans le choix des exemples. Le problème choisi doit être assez complexe pour que la méthode proposée soit acceptée comme un outil pertinent et, pour que l’outil soit opérant avec des élèves dont les acquisitions sont encore en cours de maturation, il faut que la complexité du problème soit « gérable » dans les conditions de travail de la classe.

2 Soulevons le problème (le temps de comprendre)

Consacrons un moment à la recherche d’un algorithme. Cet examen sera riche d’enseignement.

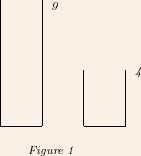
« Au moyen de deux récipients dont les capacités respectives sont neuf litres et quatre litres, nous souhaitons disposer d’une quantité d’eau de six litres »

Représentons-nous les deux récipients. Du fait de l’absence de graduation, nous ne savons pas comment mesurer exactement ; tâtonnons un peu. Le tâtonnement est la forme la plus primitive de recherche d’une solution. Nous pouvons remplir complètement le plus grand ; si, avec son contenu, nous remplissons alors le petit, il nous reste cinq litres dans le grand. Pouvons-nous également en obtenir six ? Vidons à nouveau les deux récipients. Nous pourrions aussi. . .

Nous agissons ainsi comme la plupart des gens à qui l’on pose ce problème. Nous faisons un essai, puis un autre, et, après chaque échec, nous recommençons et cherchons autre chose. En somme, nous progressons, en partant de la situation donnée au début, vers la situation finale désirée, c’est à dire en allant du connu vers l’inconnu. Il se peut qu’après maintes tentatives nous finissions par réussir, mais ce sera par hasard.

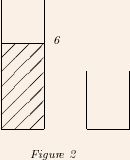
Que nous demande-t-on ? Représentons-nous la situation finale comme à la figure 2. (Partons de ce qui est demandé et admettons que ce que l’on cherche est déjà trouvé). À partir de quelle situation précédente pourrions-nous obtenir la situation désirée ; (Cherchons à partir de quel antécédent le résultat final pourrait être obtenu). Le grand récipient rempli, il faudrait en retirer trois litres exactement. Pour cela ..., il faudrait avoir déjà un litre dans le petit. Voilà l’idée ! (Cf. fig. 3) ;

Cherchons à nouveau quel pourrait être l’antécédent de cet antécédent. La situation de la figure 2 est équivalente aux situations des figures 3 et 4. Si l’on obtient l’une quelconque des situations des figures 2, 3 et 4, on obtiendra aussi bien les deux autres.

Ainsi, par raisonnement régressif nous avons découvert la succession d’opérations appropriées. Nous n’avons plus qu’à renverser le processus en partant du dernier point atteint dans notre analyse. Nous faisons les opérations suggérées par la figure 5 et obtenons la figure 4, puis nous passons à la figure 3, de là à la figure 2 et finalement à la figure 1.

Il y a certainement quelque chose d’assez profond dans cette méthode. L’obligation de s’éloigner du but, de ne pas prendre la route qui mène directement au résultat désiré, pour découvrir la succession d’opérations appropriées, suit un ordre exactement à l’inverse de l’ordre réel. Il n’est nul besoin de génie pour résoudre un problème en revenant en arrière.

Le but n’est pas le but, c’est la voie [Lao Tseu].

Chacun d’entre nous peut vérifier que les élèves en difficulté disent souvent : « Je ne sais pas comment faire ! » et qu’il nous est facile, alors, de demander : « Faire quoi ? » tant nous savons bien que c’est l’objectif qui détermine, en grande partie, le parcours. Cela est vrai pour l’algorithmique mais aussi pour résoudre les problèmes généralement... (excepté, peut-être, les problèmes financiers).

Utilisons cet acquis pour analyser une autre situation simple qui met en jeu également l’affectation. L’affectation sera la principale difficulté que nous aurons à éclaircir avec les élèves.

3 Reposons le problème (le temps d’une première conclusion)

La forme, c’est le fond qui fait surface [Victor Hugo]

J’ai essayé de systématiser la méthode précédente au moyen d’une table d’analyse, c’est le premier outil que les élèves acquerront.

Cette table d’analyse (figure 7) intervient lors de l’étape de l’écriture de l’algorithme avec un métalangage. Elle permet d’organiser méthodiquement l’expression de l’algorithme. C’est un tableau de 3 colonnes réalisant le schéma dans lequel l’algorithme s’organise et se développe. Les élèves commencent par placer en haut de la colonne centrale la dernière action, ce qui fait apparaître, au moins, une variable que l’on va chercher à expliciter. Cette variable en présuppose d’autres que l’on explicite, et ainsi de suite jusqu’à ce que toutes les variables soient expliquées ou explicitées. Dans la colonne Lexique, on précise pour chaque variable son domaine de définition. Les élèves terminent en fixant dans la colonne de droite l’ordre d’exécution des séquences pour le programme. Ainsi que le souligne Gérard Kuntz dans ses formations de « l’option informatique des lycées » cette table est constituée de 3 parties : les définitions lexicales, les définitions formelles (algorithmiques), l’ordre des définitions qui définit l’algorithme. Vous remarquerez que les définitions formelles constituent exactement un « système d’équations » (au sens mathématique) qui permet de calculer toutes les inconnues (à partir des données et des définitions). Cette remarque est tout à fait générale et fait le lien entre algorithmique et mathématiques.

Titre (Précise le résultat attendu de la suite de définitions)
Lexique	Définitions	Séquences
(2)	-1
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - ›(3)

↑	↑	↑
Explicite tous les noms symboliques identificateurs introduits dans les définitions, et précise les types manipulés.	Décrit les actions à exécuter	Ordonnance les actions pour un traitement au moyen d’un ordinateur

Exemple : « Écrire l’enchaînement des calculs donnant le poids idéal d’une personne ».

Le Poids en Kg dépend de la Taille en cm et d’un coefficient : Poids = Ecart × Coef   où Ecart représente Taille - 100

Coef est fonction du sexe Coeff = 1.1 SI Sexe = « masculin » 1 SI Sexe = « féminin »

Figure 8 Table d’analyse du calcul du poids idéal

4 Déplaçons le problème (le temps d’une deuxième conclusion)

L’algorithmique n’est ni une science expérimentale, ni un gadget pédagogique.

Nous disposons maintenant d’un guide de construction pour nos premiers algorithmes. En revanche, il nous manque un outil de validation. Nous en avons fini avec l’analyse. Pour se rendre compte de la difficulté, on peut consulter de nombreux exercices proposés sur Internet [7] .
Viendrait-il à l’idée de commencer l’étude de la résolution des équations sans, au préalable, avoir fait travailler les élèves sur la priorité des opérations ? De même, est-il prudent de faire précéder la construction d’algorithme par l’apprentissage de la lecture, de la compréhension, et de l’écriture de la suite des actions.

Un programme décrit la suite de transformations qui fait passer de la situation initiale à la situation finale, en passant par toute une suite de situations intermédiaires. Les situations peuvent être décrites au moyen de prédicats reliant les variables du programme. On va donc isoler dans la suite des situations quelques-unes d’entre elles considérées comme les « pivots » du programme, puis dire comment on passe de l’une à l’autre. Pour cela il convient de s’habituer à placer de vrais « commentaires » entre les actions, pas des paraphrases comme « // J’augmente x de 1 » qui n’apporte rien à la compréhension.

L’algorithme fait intervenir la notion de temps. « Avant » l’instruction c’est la pré-assertion, « après » c’est la post-assertion. Ces assertions décrivent des états (relation entre les variables) les instructions font passer d’un état à l’autre.

Savoir donner du sens

Sachant où l’on est, et le but à atteindre, on sait quel chemin prendre.

• Commençons avec deux exemples simples et voyons comment les commentaires qui encadrent l’affectation nous renseignent sur le sens de l’action :

  • Si a = xⁱ⁺¹ et si l’on effectue a = a × x ; on pourra écrire :

    // a = xi+1 a PRENDLAVALEUR a * x // a = xi+2

    ←- Situation de départ ; ←- la deuxième ligne indique l’action ; ←- la troisième exprime la nouvelle relation.

  • Supposons maintenant que, sans modifier ni x, ni a, nous ayons besoin d’avoir a = xⁱ⁺¹ et que le travail déjà accompli soit tel que a = xⁱ⁺² ; nous devons écrire i = i+1, ce qui demande un instant de réflexion [8] . Soit :

    // a = xi+2 i PRENDLAVALEUR i + 1 // a = xi+1

    ←- Situation tenue pour vraie ; ←- action ; ←- la relation que l’on veut atteindre.

• Le déroulement linéaire, ou enchaînement, est une succession d’instructions pour se rapprocher d’un résultat prévu ; les relations entre les variables sont modifiées. Bien entendu l’état final est le résultat de la succession des états intermédiaires

// a = xi+1 a PRENDLAVALEUR a * x i PRENDLAVALEUR i + 1 // a = xi+1

On utilisera les 2 exemples précédents pour interpréter cet enchaînement.

Les prescripteurs laissent entendre que l’épreuve de la programmation, sorte d’épreuve du réel, pourrait servir à la validation impartiale du travail de l’élève. Certes l’idée est répandue, voire même séduisante ; mais c’est un leurre. Jacques Arsac [Arsac1] en a fait une illustration remarquable dont je me suis inspiré pour montrer aux élèves qu’un programme qui fonctionne n’est pas nécessairement un algorithme correct [Dhénin 2] La principale difficulté est d’éviter de travailler à tâtons, « On error try again », il convient de donner, dès que possible, du sens à ce que l’on écrit.

L’exemple ci-dessous [9] en constitue une preuve irréfutable. Essayer un programme ne prouve pas qu’il soit juste. C’est la raison pour laquelle je tenais à l’examiner afin de montrer « comment chasser l’erreur ».

Lire x  Lire n  a PREND_LA_VALEUR x  i PREND_LA_VALEUR 0  t PREND_LA_VALEUR n    TANT_QUE (i < t) FAIRE      a PREND_LA_VALEUR a * x      i PREND_LA_VALEUR i + 1      t PREND_LA_VALEUR n - 1    FIN_TANT_QUE  AFFICHER a

Essayons ce programme avec x = 5 et n = 3 ; réponse 125. Essayons encore avec x = 4 et n = 2 ; réponse 16. La première ligne de TANT_QUE a = a×x montre bien que l’on calcule xn par multiplications successives. Nous pouvons être satisfaits et nous arrêter là. Pourtant, un dernier essai avec x = 10 et n = 1 s’avère poser problème.

Construire une boucle

Dès que le programme comporte une boucle, les choses se compliquent singulièrement. Il devient très difficile de « penser » le déroulement, notamment la condition d’arrêt [Dhénin 2]. Il n’est pas facile de corriger le programme ci-dessus. Il est probable que l’auteur a mal choisi son test d’arrêt et qu’il a cherché à redresser la situation en introduisant la variable t. Son calcul dans la boucle est inattendu. Les deux exemples du § précédent s’appliquent ici pour donner l’interprétation.

Pour éviter de passer un temps considérable à rechercher une erreur d’algorithme, il est préférable d’apprendre la méthode de construction. Supposons que l’on ait fait une partie du travail et calculé a = xⁱ pour i ≤ n, si i = n, c’est fini ; sinon, il faut se rapprocher de la solution en faisant croître i par a = a × x et i = i + 1. Reste à voir le démarrage, c’est à dire trouver des valeurs de a et i telles que l’assertion a = xⁱ soit vérifiée pour n positif ou nul. Nous prendrons i = 0 et a = x⁰ = 1 ; d’où le nouveau programme :

Lire x  Lire n  a PREND_LA_VALEUR 1  i PREND_LA_VALEUR 0    TANT_QUE (i < n) FAIRE  // a = x^i      a PREND_LA_VALEUR a * x  // a = x^i+1      i PREND_LA_VALEUR i + 1  // a = x^i    FIN_TANT_QUE  AFFICHER a

Démarrer  le processus i = 0 et a = x0 = 1 Voir  si c’est fini i = n, Proposer  une situation générale : a = xi Progresser  vers la solution et rétablir la situation générale a = a × x et i = i + 1 Interpréter le résultat, Examiner le programme pour en chasser les calculs inutiles ; on pourra, ici, supprimer le calcul de t.

Cet exemple appelle quelques remarques :

• Les commentaires sont nécessaires à la compréhension non seulement pour la relecture, mais même au moment de la rédaction.

• La mise au point et la recherche d’erreur ne se font pas quand tout est écrit. Ils se font au fur et à mesure. comme dans les devoirs de math.

• Un algorithme n’est pas écrit pour être lu par un ordinateur, mais par un humain ; il doit être clair et simple

5 Ce n’est qu’un début...

Beaucoup d’entre nous se demandent : « Que peut m’apporter l’enseignement de ce nouveau chapitre ? ». Pour ma part, j’ai trouvé une première réponse en disant que la recherche de résolution d’un problème de math peut être renforcée par l’apprentissage de la méthode de construction d’un algorithme. Identifier ce que l’on cherche [10] et remonter jusqu’aux données [11] .

En ce qui concerne l’algorithmique elle-même, son apprentissage ne se résume pas au b-a-ba. Comme en mathématique ; assortir son discours d’un vocabulaire inhérent à la matière ne suffit pas, il y a un mode de penser à s’approprier. L’exposé hypothético-déductif qui fait suite à l’exclamation "Ha, ça y est, j’ai trouvé !" est long à métaboliser. On ne se contentera pas de programmer. Ce n’est pas cela l’algorithmique.

L’algorithmique, elle aussi, nous renvoie à la question du sens. Sur ce le sujet, difficile, elle illustre l’idée que c’est l’acte de traduire qui donne un sens. Traduire une équation de fonction par un dessin, traduire un problème par un système d’égalités ou traduire un algorithme par un programme il est toujours question de traduire pour comprendre. L’usage des assertions est un pas dans cet apprentissage.

Références

[Lao Tseu]   Lao tseu http ://chroniquestaoistes.free.fr/html/lao_tseu001.html

[Khawarizmi]   Al-Khawarizmi, WIKIPEDIA http ://fr.wikipedia.org/wiki/Al-Khawarizmi

[Vuillemin]   La philosophie de l’Algèbre. J. VUILLEMIN, P.U.F., Paris, 1962 http ://www.univ-irem.fr/commissions/epistemologie/ressouces/ress.ext/themes/algebre.htm

[Arsac1]    Les bases de la programmation Jacques Arsac

[Arsac2]    Préceptes pour programmer Jacques Arsac

[Kernigham]   The Practice of Programming Kernigham and Pike

[Ledgard]   Proverbes de programmation H. F. Ledgard

[Mathadoc]   Mathadoc http ://www.mathadoc.com/Documents/college/3eme/3arithm/activ5.PDF

[Eduscol]    Eduscol http ://eduscol.education.fr/D0015/Doc_ress_algo_v25.pdf

[Sesamath]   Sesamath http ://revue.sesamath.net/spip.php ?article216

[Leguay]    Les maths selon Stella Baruck Olivier LEGUAY, octobre 2008 http ://www.paperblog.fr/1156875/les-maths-selon-stella-baruck/

[Brachet]    AlgoBox 2009/2010 Pascal Brachet L’auteur est professeur de mathématiques au lycée Bernard Palissy à Agen
http ://www.xm1math.net/algobox/index.html

[Bkouche]   Des tice dans l’enseignement des mathématiques, Rudoph Bkouche, octobre 2009, http ://www.univ-irem.fr/spip.php ?article282

[Dhenin1]   Carte mentale http ://algotaf.free.fr/Maps/AlgoSeconde.html

[Dhenin2]   Un exemple de boucle erronée en AlgoBox, DHÉNIN, 2009 http ://algotaf.free.fr/Code_Faux.html

[Dhenin3]   Correction d’un programme faux. DHÉNIN http ://algotaf.free.fr/tri_faux.correction.pdf